YUV

YUV の計算をしていてふと気がついた。この行列ちゃんと直交しているのだろうか？

で手計算でやってみるとなるほど直交している。Y の方角は 257,504,98 なわけだが、本当にRGB を等しくしようとすると 333,333,333 になりそうなものだが、そうしていない。G をもうチョイ多くして 3,4,3 でもない。B なんて 98 ÷ ( 257 + 504 + 98 ) ≒ 0.114 で本来グレースケールの 1/3 くらいしか寄与していない。等分にしたグレースケールと YUV のグレースケールを比べてみたい気もする。
ITU 601 によると Y は は 16 〜 235 で UV は 16 〜 240 までとなっている。257 + 504 + 98 = 859 で 1000 にならないが、これに 256 / (235 - 16 + 1) をかけるとほぼ 1000 になる。UV も同様。つまり YUV はダイナミックレンジ（という言葉をここで使っていのかどうか）が圧縮されているわけだ。SA7115H は YUV も 0x00 と 0xFF を除く １〜254 までをデータとして使っているようなので、折角の解像度も単純に計算してしまうとオーバフロー・アンダーフローで消えてしまう。ちゃんと係数を考えないといけない。
さて、三次元で考えるとちょっとむずかしいので二次元で考える。ついでに Y の方角が微妙にずれているとめんどくさいので 45度で考える。でもとの座標が X, Y のレンジがそれぞれ 0 〜 1.0 だとすると、絵的には次のようになる。

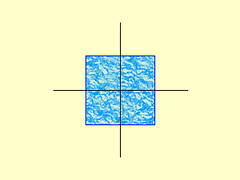
これに45度ずれた座標を重ね合わせる。そして、45度傾ける。

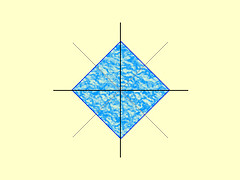
(1.0, 1.0) の座標は (0, 1.414) になる。ここでオーバフローするのでその分縮小する。あからさまにわかるのは変換した座標系の面積は倍になっていて、元の座標系のレンジでは到達できない場所があるということ。到達できないのはともかく、変換した座標系のレンジを同じようにしようとすると縮小する必要があり、その分、密度が落ちてしまうということ。あまり問題にならないのかもしれないが、密度が落ちれば精度が下がるわけで、計算した結果その近くのきりのいい値にまるめられる。RGB -> YUV -> RGB とかするとどんどん値がずれていくに違いない。

いいのか？それで。これを防ぐためにはダイナミックにビットをアサインしないといけないだろう。例えば Y 成分が０から遠ざかれば Y の精度が上がりレンジが増え、逆に UV のレンジが狭くなる。まぁそこまでしなくても良いということなのでしょう。

あと計算していて気がついたのだが、X、Y、Z の順に 45度で回転させれば等分の方角になるかと思ったけど違うのね。lisp で書けばいいのかもしれないけど、記号処理（というほどのものではない）を簡単に C で書いてしまった。

char *
plus(char *str0, char *str1)
{
        char buf[256];
        if (( str0 == 0 ) && (str1 != 0)) {
                return str1;
        }
        if (( str0 != 0 ) && (str1 == 0)) {
                return str0;
        }
        if (( str0 == 0 ) && (str1 == 0)) {
                return 0;
        }
        sprintf(buf, "(%s + %s)", str0, str1);
        return strdup(buf);
}

char *
plus3(char *str0, char *str1, char *str2)
{
        return plus(plus(str0, str1), str2);
}

char *
mul(char *str0, char *str1)
{
        char buf[256];
        if (( str0 == 0 ) || (str1 == 0)) {
                return 0;
        }
        if ( is_one(str0) && is_one(str1) ) {
                return ONE;
        }
        if ( is_one(str0) ) {
                return str1;
        }
        if ( is_one(str1) ) {
                return str0;
        }
        sprintf(buf, "%s * %s", str0, str1);
        return strdup(buf);
}

何を書いているかわからないだろうが、、、次のマトリックスをいれると

char *m0[3][3] =
{
        { "1", 0, 0 },
        { 0, "cos0", "sin0" },
        { 0, "-sin0", "cos0" },
};

char *m1[3][3] =
{
        { "cos1", 0, "-sin1" },
        { 0, "1", 0 },
        { "sin1", 0, "cos1" },
};

char *m2[3][3] =
{
        { "cos2", "sin2", 0 },
        { "-sin2", "cos2", 0 },
        { 0, 0, "1" },
};

結果として次のマトリックスを吐き出す。

---begin---
cos1 * cos2
cos1 * sin2
-sin1
(sin0 * sin1 * cos2 + cos0 * -sin2)
(sin0 * sin1 * sin2 + cos0 * cos2)
sin0 * cos1
(cos0 * sin1 * cos2 + -sin0 * -sin2)
(cos0 * sin1 * sin2 + -sin0 * cos2)
cos0 * cos1
---end---

手計算でやるよりずっと早くて正確だ。手計算では何度も間違えたぞ。